Hidrostatica e Hidrodinamica
INTRODUCCIÓN
Desde el punto de vista macroscópico, se acostumbra clasificar la materia, en sólidos y fluidos. Un fluido, es una sustancia que puede fluir, de tal forma que el término fluido incluye a los líquidos y los gases. Aun la distinción entre un líquido y un gas no es tajante, en virtud de que, cambiando en forma adecuada la presión y la temperatura resulta posible transformar un líquido en un gas o viceversa; durante el proceso la densidad, la viscosidad y otras propiedades cambian de manera continua.
En un sentido estricto, se puede considerar un fluido como un conjunto de moléculas distribuidas al azar que se mantienen unidas a través de fuerzas cohesivas débiles y las fuerzas ejercidas por las paredes del recipiente que lo contiene. La rama de la física que estudia los fluidos, recibe el nombre de mecánica de los fluidos, la cual a su vez tiene dos vertientes: hidrostática, que orienta su atención a los fluidos en reposo; e hidrodinámica, la cual envuelve los fluidos en movimiento.
En este material instruccional, se describirá brevemente algunas propiedades de los fluidos: densidad, peso específico, volumen específico entre otras; nuevos principios físicos serán presentados para explicar efectos como la fuerza de flotación (boyantez) sobre un objeto sumergido. Deduciremos una expresión para la presión ejercida por un fluido en reposo como una función de la densidad y profundidad; con ello, nos introduciremos al campo de la manometría.
Al estudiar los fluidos en movimientos, se presentará la ecuación de continuidad, examináremos y aplicaremos el Principio de Bernoulli en la resolución de problemas que involucren fluidos en movimiento. Se dará una introducción al concepto de pérdidas hidráulicas en tuberías y su relación con la Ley de Conservación de la Energía Mecánica descrita en el Módulo III de Física I. Al final, se ofrecerá una recopilación de algunos problemas que han formado parte de las evaluaciones de cohortes precedentes.
Al término de éste módulo, el estudiante tendrá la habilidad y pericia necesaria para aplicar los conceptos básicos de hidrostática e hidrodinámica a problemas prácticos que involucren fluidos newtonianos.
- Propiedades físicas de los fluidos: densidad, peso específico, volumen específico, viscosidad y gravedad específica.
- Principio fundamental de la hidrostática.
- Principio de Arquímedes (Boyantez).
- Principio de Pascal (Prensa hidráulica).
- Fuerzas ejercidas sobre superficies planas sumergidas: fuerza de presión.
- Momento de inercia: centro de presión.
- Ecuación de continuidad.
- Régimen de flujo: laminar, transición y turbulento.
- Teorema de Bernoulli y Teorema de Torricelli.
CONOCIMIENTOS PREVIOS
- Cálculo integral: aplicaciones de integrales definidas con condiciones iniciales.
- Cálculo integral: área debajo de una curva.
- Trigonometría plana: resolución de triángulos.
- Funciones matemáticas: graficación.
DESARROLLO TEÓRICO
La hidrostática es una rama de la física que se encarga del estudio de los fluidos carentes de movimiento.
1.2 Propiedades de los fluidos.
Densidad: Es la masa contenida en una unidad de volumen de una sustancia (masa por unidad de volumen). Cuando se trata de una sustancia homogénea, la expresión para su cálculo es: 
(1)
Donde
: densidad de la sustancia, Kg/m3
m: masa de la sustancia, Kg
V: volumen de la sustancia, m3
En el caso de sustancias no homogéneas se usa las siguientes fórmulas:
Densidad en un punto: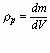 
(2)
Densidad promedia: (3)
Las unidades en las cuales se suele expresar la densidad son: Kg/m3, Kg/dm3, gr/cm3 y lb/pie3
La densidad de una sustancia varía con la temperatura y la presión; al resolver cualquier problema debe considerarse la temperatura y la presión a la que se encuentra el fluido.
El agua posee una densidad absoluta a 4 º C y una atmósfera de presión igual a 999,997 Kg/m3 o 62,244 lb/pie3
Tabla 1. Variación de algunas propiedades físicas del agua con la temperatura.
Temperatura (ºC) | Peso específico (KN/m3) | Densidad (Kg/m3) |
0 | 9,805 | 999,8 |
5 | 9,807 | 1.000 |
10 | 9,804 | 999,7 |
15 | 9,798 | 999,1 |
20 | 9,789 | 998,2 |
25 | 9,777 | 997,0 |
30 | 9,764 | 995,7 |
40 | 9,730 | 992,2 |
50 | 9,689 | 988,0 |
60 | 9,642 | 983,2 |
70 | 9,589 | 977,8 |
80 | 9,530 | 971,8 |
90 | 9,466 | 965,3 |
100 | 9,399 | 958,4 |
Nota: los valores se dan a presión atmosférica.
Por lo general, se suele conocer la gravedad específica del fluido, no su densidad absoluta. La gravedad específica se define como la relación entre el peso de una sustancia y el de un volumen igual de agua en condiciones estándar (4 º C, 1 atm). La gravedad específica se conoce también como densidad relativa o peso específico relativo, se representa con la letra "s"
(4)
Donde:
Wo: peso de un volumen igual al volumen de la sustancia de agua a 4 ºC y 1 atmósfera
: peso específico del agua a 4 º C y 1 atmósfera; = 9806,26 N/m3 = 62,244 lb/pie3
: densidad del agua a 4 º C y 1 atmósfera; = 999,997 Kg/m3 = 62,244 lb/pie3
Es importante señalar que la gravedad específica es adimensional.
Peso específico: Peso por unidad de volumen de una sustancia.
Cuando se trata de una sustancia homogénea, la expresión para su cálculo es: 
; en el caso de sustancias no homogéneas se usa las siguientes fórmulas:
Peso específico en un punto: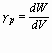 
(5)
Peso específico promedia: 
(6)
Las unidades en las cuales se suele expresar son: N/m3, Kgf/m3, dina/cm3 y lbf/pie3
Viscosidad dinámica o absoluta o newtoniana o coeficiente de viscosidad (
): Es la medida de la resistencia de un fluido a ser deformado por esfuerzos cortantes
(7)
Donde:
: esfuerzo cortante aplicado, N/m2
: rapidez de deformación angular producida, Rad/s
Las unidades usuales son: N.s/m2(Pa.s), dina.s/cm2(poise), Kgm/m.s, lbf.s/pie2
Viscosidad cinemática o relativa (
): Es la medida de la resistencia de un fluido a ser deformado por esfuerzos cortantes.
(8)
Unidades usuales: m2/s, cm2/s(stoke), pie2/s
Existen muchas más propiedades físicas como: volumen específico, presión de vapor, tensión superficial y el módulo de elasticidad volumétrico las cuales se abordarán con mayor profundidad en subproyectos ulteriores.
Presión en mecánica, es la fuerza por unidad de superficie que ejerce un líquido o un gas perpendicularmente a dicha superficie.
La presión suele medirse en atmósferas (atm); en el Sistema Internacional de unidades (SI), la presión se expresa en Newton por metro cuadrado; un Newton por metro cuadrado es un pascal (Pa). La atmósfera se define como 101.325 Pa, y equivale a 760 mm de mercurio o 14,70 lbf/pulg2 (denominada psi).
(9)
Donde:
P: presión ejercida sobre la superficie, N/m2
F: fuerza perpendicular a la superficie, N
A: área de la superficie donde se aplica la fuerza, m2
La mayoría de los medidores de presión, o manómetros, miden la diferencia entre la presión de un fluido y la presión atmosférica local. Para pequeñas diferencias de presión se emplea un manómetro que consiste en un tubo en forma de U con un extremo conectado al recipiente que contiene el fluido y el otro extremo abierto a la atmósfera. El tubo contiene un líquido, como agua, aceite o mercurio, y la diferencia entre los niveles del líquido en ambas ramas indica la diferencia entre la presión del recipiente y la presión atmosférica local.
Para diferencias de presión mayores se utiliza el manómetro de Bourdon, llamado así en honor al inventor francés Eugène Bourdon. Este manómetro está formado por un tubo hueco de sección ovalada curvado en forma de gancho. Los manómetros empleados para registrar fluctuaciones rápidas de presión suelen utilizar sensores piezoeléctricos o electrostáticos que proporcionan una respuesta instantánea.
Como la mayoría de los manómetros miden la diferencia entre la presión del fluido y la presión atmosférica local, hay que sumar ésta última al valor indicado por el manómetro para hallar la presión absoluta. Una lectura negativa del manómetro corresponde a un vacío parcial.
Las presiones bajas en un gas (hasta unos 10-6 mm de mercurio de presión absoluta) pueden medirse con el llamado dispositivo de McLeod, que toma un volumen conocido del gas cuya presión se desea medir, lo comprime a temperatura constante hasta un volumen mucho menor y mide su presión directamente con un manómetro. La presión desconocida puede calcularse a partir de la ley de Boyle-Mariotte. Para presiones aún más bajas se emplean distintos métodos basados en la radiación, la ionización o los efectos moleculares.
1.4 Principio fundamental de la hidrostática.
La diferencia de presión entre dos puntos de un mismo líquido es igual al producto del peso específico del líquido por la diferencia de niveles
P2 - P1 = 
. (h2 - h1) (10)
Donde:
P2, P1: presión hidrostática en los puntos 2 y 1 respectivamente, N/m2
h2, h1: profundidad a la que se encuentran los puntos 2 y 1 respectivamente, m
: peso específico del fluido, N/m3
1.5 Principio de Pascal.
Toda presión ejercida sobre la superficie libre de un líquido en reposo se transmite íntegramente y con la misma intensidad a todos los puntos de la masa líquida y de las paredes del recipiente.
1.6 Principio de Arquímedes (Boyantez).
Todo cuerpo sumergido en un líquido, recibe un empuje de abajo hacia arriba igual al peso del líquido desalojado.
E = . V (11)
Donde:
E: empuje hidrostático, N
: peso específico del fluido, N/m3
V: volumen de fluido desalojado por el cuerpo, m3
El concepto de "peso aparente" se refiere al "peso supuesto" que posee un cuerpo que se encuentra sumergido en un fluido.
Pa = W – E (12)
Donde:
Pa: peso aparente, N
W: peso real del cuerpo, N
E: empuje hidrostático que recibe el cuerpo
El momento de inercia es la resistencia que un cuerpo en rotación opone al cambio de su velocidad de giro. A veces se denomina inercia rotacional. El momento de inercia desempeña en la rotación un papel equivalente al de la masa en el movimiento lineal.
Por ejemplo, si una catapulta lanza una piedra pequeña y una grande aplicando la misma fuerza a cada una, la piedra pequeña se acelerará mucho más que la grande. De modo similar, si se aplica un mismo par de fuerzas a una rueda con un momento de inercia pequeño y a otra con un momento de inercia grande, la velocidad de giro de la primera rueda aumentará mucho más rápidamente que la de la segunda.
El momento de inercia de un objeto depende de su masa y de la distancia de la masa al eje de rotación. Por ejemplo, un volante de 1 kg con la mayoría de su masa cercana al eje tendrá un momento de inercia menor que otro volante de 1 kg con la mayoría de la masa cercana al borde exterior.
El momento de inercia de un cuerpo no es una cantidad única y fija (Tabla 2). Si se rota el objeto en torno a un eje distinto, en general tendrá un momento de inercia diferente, puesto que la distribución de su masa con relación al nuevo eje es normalmente distinta.
Las leyes del movimiento de los objetos en rotación son equivalentes a las leyes del movimiento de los objetos que se mueven linealmente (el momento de inercia sustituye a la masa, la velocidad angular a la velocidad lineal)
El elemento de inercia de un elemento de área respecto a un eje en su plano está dado por el producto del área del elemento y el cuadrado de la distancia entre el elemento y el eje. En la Figura 1, el momento de inercia dIx del elemento respecto al eje x es:
(13)
Donde:
dIx: momento de inercia respecto del eje X.
y: distancia desde el eje x al diferencial de área.
dA: diferencial de área.
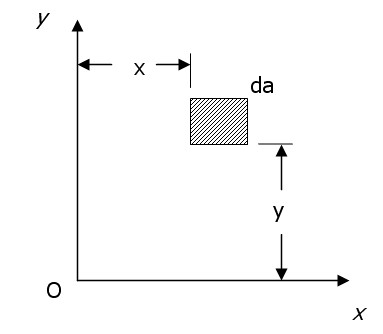
Figura 1. Un diferencial de área ubicado a una distancia x con respecto al eje y, y una distancia y respecto al eje x
Respecto al eje y, el momento de inercia es:
(14)
Donde:
dIy: momento de inercia respecto del eje Y.
x: distancia desde el eje y al diferencial de área.
dA: diferencial de área.
El momento de inercia de un área finita respecto a un eje en su plano es la suma de los momentos de inercia respecto de ese eje de todos los elementos de área contenidos en él. También se halla, frecuentemente, por medio de una integral. Si se representa por Ix este momento de inercia, tenemos:
(15)
(16)
Las unidades del momento de inercia son la cuarta potencia de una longitud; por ejemplo: cm4, m4
Es importante para el cálculo de momento de inercia en una figura plana conocer el Teorema de los ejes paralelos; el cual dice que el momento de inercia de una superficie respecto a un eje cualquiera es igual al momento de inercia respecto a un eje paralelo que pasa por el centro de gravedad, más el producto del área por el cuadrado de la distancia entre los dos ejes. Para la superficie de la Figura 2, los ejes xG e yG pasan por el centro de gravedad y los x e y son paralelos a ellos y están situados a las distancias x1 e y1. Sea A el área de la figura, IxG e IyG los momentos de inercia respecto a los ejes del centro de gravedad e Ix, Iy los correspondientes a los ejes x e y tenemos que:
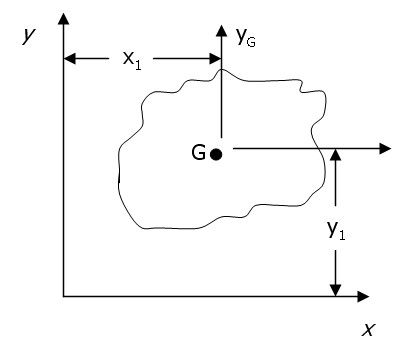
Figura 2. Una figura plana cuyo centro de gravedad se encuentra a una distancia x1 del eje y, y una distancia y1 del eje x.
(17)
(18)
Tabla 2. Momentos de inercias más comunes.
Forma de la compuerta | Momento de inercia referido al centroide |
Rectangular |
|
Cuadrada |
|
Circular |
|
b: ancho, h: alto
b: lado
r: 1.8 Presión sobre superficies planas.
La presión en el seno de un líquido en reposo se ejerce siempre normalmente a la superficie, de tal modo que si tuviéramos un vaso que contiene un líquido y hacemos orificios en varios puntos del vaso, el líquido saldría en chorros cuyas direcciones son normales a las paredes (durante un corto trayecto por supuesto) en los puntos de salida (Figura 3).
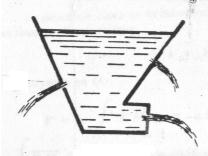
Figura 3. Depósito cónico al cual se la realizado diferentes perforaciones.
Supongamos que una superficie rectangular sumergida en el seno de un líquido, y a la que pondremos en diferentes posiciones con respecto a la superficie libre del líquido.
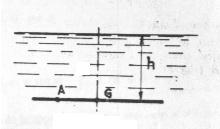
Figura 4. Superficie plana colocada paralela con respecto a la superficie libre.
Primero la supondremos paralela a la superficie libre, sumergida a una profundidad h. La presión en todos los puntos de esa superficie es la misma, es decir, es uniforme. Para calcular el valor de la presión es necesario conocer la profundidad h y el peso especifico del líquido. Llamando A a un punto cualquiera de la superficie en cuestión, tenemos:
PA = . h (19)
Para calcular la fuerza que obra sobre toda la superficie S (empuje del líquido sobre la superficie), que llamaremos F, tenemos:
F = . h . S (20)
En la expresión anterior S es la superficie y debe tenerse cuidado de no confundir el empuje con la presión. Si la presión es uniforme sobre una superficie determinada, la resultante de las fuerzas que se están ejerciendo sobre cada punto es el empuje o fuerza total y pasa por el centro de gravedad de la superficie.
F se interpreta diciendo que "cuando la presión es uniforme sobre una superficie plana, el empuje tiene un valor igual a la intensidad de la presión en cualquier punto, multiplicado por la superficie". El empuje queda representado por un vector normal a la superficie, que pasa por el centro de gravedad de ésta.
Consideremos ahora una superficie pero inclinada con respecto a la superficie libre del líquido. Aquí la presión no es uniforme en todos los puntos de la superficie, sino que va variando siendo menor en A y aumentando hasta B (Figura 5).
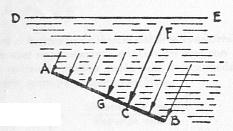
Figura 5. Distribución de las fuerzas debida a una columna de líquido en una superficie plana inclinada
El empuje debe ser normal a la superficie y ya no pasa por el centro de gravedad de ésta sino más abajo porque la resultante del sistema de fuerzas paralelas formado por las distintas presiones estará cerca de las fuerzas de mayor intensidad. El punto por donde pasa el empuje que el líquido ejerce sobre la superficie se llama "centro de presión".
Para que quede determinado el empuje es necesario determinar primero su intensidad y enseguida la localización del centro de presión.
En la Figura 6 se muestran las proyecciones de cualquier superficie plana AB sujeta a la presión estática de un líquido con superficie libre. La superficie AB hace un ángulo cualquiera con la horizontal; prolongado el plano de esa superficie, intercepta la superficie libre del líquido según una recta XX’ mostrada como un punto M en (a).
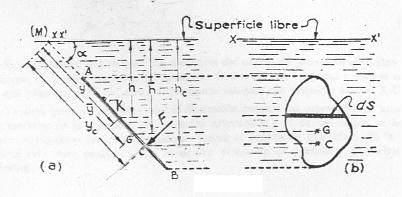
Figura 6. Superficie plana sumergida en el seno de un líquido
Supongamos que una faja elemental de la superficie tomada paralelamente al eje XX’. La presión sobre esta faja es uniforme y a su empuje podemos llamar dF. La resultante de las dF es una fuerza que ya dijimos, cae en el centro de presión; se tiene:
(21)
(22)
La superficie plana en su intersección con la superficie libre da una línea que es interesante considerar:
(23)
por sustitución, nos queda...
(24)
por cierto, que 
es el momento estático de la superficie S con respecto al eje XX’, por lo tanto:
(25)
por sustitución, nos queda...
(26)
pero como;
; por lo que al sustituir...
(27)
"El empuje o fuerza de presión sobre la superficie plana, tiene por valor el producto de la presión en el centro de gravedad por la superficie considerada", o sea:
(28)
Donde:
: peso específico del fluido en el que se encuentra sumergido la superficie libre.
: profundidad a la que se encuentra el centro de gravedad de la superficie libre.
A: área de la compuerta
La distancia del centro de gravedad de la superficie al centro de presión se calcula:
(29)
Donde:
Ic : momento de inercia de la superficie respecto al centroide
yc: distancia desde el centro de gravedad a la superficie libre en la dirección de inclinación de la compuerta
A: área total de la superficie sumergida
Es la rama de la física que se encarga del estudio de los fluidos animados de movimiento.
1.10 Gasto volumétrico y la ecuación de continuidad.
El gasto volumétrico o caudal es el volumen de agua que pasa a través de una sección de tubería por unidad de tiempo. Se expresa en m3/s, Lt/s, Pie3/s dependiendo del sistema de unidades en que se trabaje.
(30)
Donde:
Q: gasto volumétrico, m3/s
v: velocidad promedia del fluido en la sección transversal de estudio, m/s
A: superficie de la sección transversal, m2
t: tiempo en que circula en volumen V a través de la sección de estudio, s
V: volumen que atraviesa la sección transversal, m3
Cuando el gasto es igual en todas las secciones de un conducto, se dice que el régimen del escurrimiento es permanente.
Cuando el régimen es permanente y el conducto tiene diámetro variable, la velocidad es diferente en cada sección e inversamente proporcional a ella, de tal manera que:
(31)
La anterior expresión se conoce como "Ecuación de continuidad"
A medida que un fluido se mueve por un tubo de sección transversal y altura variable, la presión cambia a lo largo del mismo. En 1738, el físico suizo Daniel Bernoulli dedujo por vez primera una expresión que relaciona la presión con la velocidad y elevación del fluido.
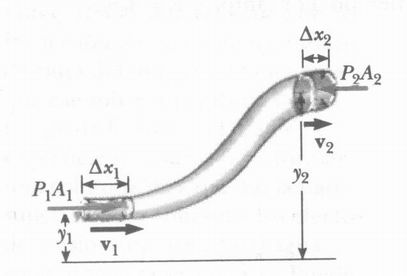
Figura 7. El fluido en la sección de longitud Δx1 se mueve en la sección de longitud Δx2. Los volúmenes de fluidos en las dos secciones son iguales.
1.12 Número de Reynolds y los regimenes de flujo.
El número de Reynolds es un número adimensional que se utiliza en la mecánica de fluidos para estudiar el movimiento de un fluido en el interior de una tubería, o alrededor de un obstáculo sólido. Se representa por R. El número de Reynolds puede ser calculado para cada conducción recorrida por un determinado fluido y es el producto de la velocidad, la densidad del fluido y el diámetro de la tubería dividido entre la viscosidad del fluido.
Para un mismo valor de este número el flujo posee idénticas características cualquiera que sea la tubería o el fluido que circule por ella. Si R es menor de 2.100 el flujo a través de la tubería es siempre laminar; cuando los valores son superiores a 2.100 el flujo es turbulento.
De acuerdo con la expresión del número de Reynolds, cuanto más elevada sea la viscosidad de un fluido mayor podrá ser el diámetro de la tubería sin que el flujo deje de ser laminar, puesto que las densidades de los líquidos son casi todas del mismo orden de magnitud. Por este motivo los oleoductos, en régimen laminar, pueden tener secciones superiores a las conducciones de agua, ya que la viscosidad de los fluidos que circulan por aquéllos es mayor que la del agua.
(38)
Donde:
NRe: Número de Reynold, adimensional
V: velocidad media del fluido, m/s
p: densidad media del fluido, Kg/m3
D: diámetro interno de la tubería, m
m: viscosidad absoluta del fluido, N.s/m2
COMENTARIOS
MECANICA DE FLUIDOS
Un fluido es un lìquido o un gas. La caracterìstica principal de un fluido es su incapacidad para resistir fuerzas cortantes.
En mècanica de fluidos se estudia el comportamiento de lìquidos y gases, especialmente los lìquidos , en dos condiciones :
1. Liquidos en Reposo : Hidrostática
2. Lìquidos en Movimiento : Hidrodinámica
0 comentarios