Histrostatica e hidrodinamica
Hidroestática
Todas las presiones representan una medida de la energía potencial por unidad de volumen en un fluido
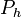 , Presión hidrostática.
, Presión hidrostática. 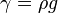 , Peso específico.
, Peso específico. 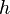 profundidad bajo la superficie del fluido.
profundidad bajo la superficie del fluido.
- La presión hidrodinámica es la presión termodinámica dependiente de la dirección considerada alrededor de un punto que dependerá además del peso del fluido, el estado de movimiento del mismo.
Presión hidrostática
Un fluido pesa y ejerce presión sobre las paredes, sobre el fondo del recipiente que lo contiene y sobre la superficie de cualquier objeto sumergido en él. Esta presión, llamada presión hidrostática, provoca, en fluidos en reposo, una fuerza perpendicular a las paredes del recipiente o a la superficie del objeto sumergido sin importar la orientación que adopten las caras. Si el líquido fluyera, las fuerzas resultantes de las presiones ya no serían necesariamente perpendiculares a las superficies. Esta presión depende de la densidad del líquido en cuestión y de la altura a la que esté sumergido el cuerpo y se calcula mediante la siguiente expresión:
Donde, usando unidades del SI,
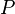 es la presión hidrostática (en pascales);
es la presión hidrostática (en pascales);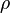 es la densidad del líquido (en kilogramos sobre metro cúbico);
es la densidad del líquido (en kilogramos sobre metro cúbico);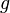 es la aceleración de la gravedad (en metros sobre segundo al cuadrado);
es la aceleración de la gravedad (en metros sobre segundo al cuadrado);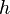 es la altura del fluido (en metros). Un liquido en equilibrio ejerce fuerzas perpendiculares sobre cualquier superficie sumergida en su interior
es la altura del fluido (en metros). Un liquido en equilibrio ejerce fuerzas perpendiculares sobre cualquier superficie sumergida en su interior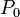 es la presión atmosférica
es la presión atmosférica
Presión hidrodinámica
En un fluido en movimiento general, al medir la presión según diferentes direcciones alrededor de un punto esta no será constante, dependiendo la dirección donde la presión es máxima y mínima de la dirección y valor de la velocidad en ese punto.
De hecho en un fluido newtoniano cuya ecuación constitutiva, que relaciona el tensor tensión con el tensor velocidad de deformación:
Donde:
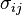 son las componentes del tensor tensión.
son las componentes del tensor tensión.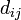 son las componentes del tensor velocidad de deformación.
son las componentes del tensor velocidad de deformación.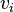 son las componentes del vector velocidad del fluido.
son las componentes del vector velocidad del fluido.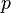 es la presión hidrodinámica.
es la presión hidrodinámica.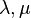 son dos viscosidades que caracterizan el comportamiento del fluido.
son dos viscosidades que caracterizan el comportamiento del fluido.
Puede probarse que la presión hidrodinámica se relaciona con la presión media por:
Donde:
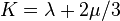 , es la viscosidad volumétrica.
, es la viscosidad volumétrica.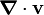 , es la divergencia del vector velocidad.
, es la divergencia del vector velocidad.
La hidrostática es la rama de la mecánica de fluidos que estudia los fluidos en estado de equilibrio, es decir, sin que existan fuerzas que alteren su movimiento o posición. Los principales teoremas que respaldan el estudio de la hidrostática son el principio de Pascal y el principio de Arquímedes.
Principio de Pascal
En física, el principio de Pascal es una ley enunciada por el físico y matemático francés Blaise Pascal (1623-1662) que se resume en la frase: «el incremento de la presión aplicada a una superficie de un fluido incompresible-líquido-, contenido en un recipiente indeformable, se transmite con el mismo valor a cada una de las partes del mismo». Es decir, que si se aplica presión a un líquido no comprimible en un recipiente cerrado, ésta se transmite con igual intensidad en todas direcciones y sentidos. Este tipo de fenomeno se puede apreciar, por ejemplo en la prensa hidráulica la cual funciona aplicando este principio.
Principio de Arquímedes
El principio de Arquímedes establece que cualquier cuerpo sólido que se encuentre sumergido total o parcialmente (depositado) en un fluido será empujado en dirección ascendente por una fuerza igual al peso del volumen del liquido desplazado por el cuerpo sólido.
El objeto no necesariamente ha de estar completamente sumergido en dicho fluido, ya que si el empuje que recibe es mayor que el peso aparente del objeto, éste flotará y estará sumergido sólo parcialmente.
| ||||||||
Hidrodinámica

La hidrodinámica estudia la dinámica de fluidos incompresibles. Por extensión, dinámica de fluidos.
Etimológicamente, la hidrodinámica es la dinámica del agua, puesto que el prefijo griego "hidro-" significa "agua". Aun así, también incluye el estudio de la dinámica de otros fluidos. Para ello se consideran entre otras cosas la velocidad, presión, flujo y gasto del fluido. Para el estudio de la hidrodinámica normalmente se consideran tres aproximaciones importantes:
- Que el fluido es un líquido incompresible, es decir, que su densidad no varía con el cambio de presión, a diferencia de lo que ocurre con los gases.
- Se considera despreciable la pérdida de energía por la viscosidad, ya que se supone que un líquido es óptimo para fluir y esta pérdida es mucho menor comparándola con la inercia de su movimiento.
- Se supone que el flujo de los líquidos es en régimen estable o estacionario, es decir, que la velocidad del líquido en un punto es independiente del tiempo.
La hidrodinámica tiene numerosas aplicaciones industriales, como diseño de canales, construcción de puertos y presas, fabricación de barcos, turbinas, etc.
El gasto o caudal es una de las magnitudes principales en el estudio de la hidrodinámica. Se define como el volumen de líquido ΔV que fluye por unidad de tiempo Δt. Sus unidades en el Sistema Internacional son los m3/s y su expresión matemática:
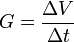
Esta fórmula nos permite saber la cantidad de líquido que pasa por un conducto en cierto intervalo de tiempo o determinar el tiempo que tardará en pasar cierta cantidad de líquido.
El principio de Bernoulli es una consecuencia de la conservación de la energía en los líquidos en movimiento. Establece que en un líquido incompresible y no viscoso, la suma de la presión hidrostática, la energía cinética por unidad de volumen y la energía potencial gravitatoria por unidad de volumen, es constante a lo largo de todo el circuito. Es decir, que dicha magnitud toma el mismo valor en cualquier par de puntos del circuito. Su expresión matemática es:
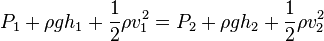
donde P es la presión hidrostática, ρ la densidad, g la aceleración de la gravedad, h la altura del punto y v la velocidad del fluido en ese punto. Los subíndices 1 y 2 se refieren a los dos puntos del circuito.
La otra ecuación que cumplen los fluidos no compresibles es la ecuación de continuidad, que establece que el caudal es constante a lo largo de toda el circuito hidráulico:
G = A1v1 = A2v2
donde A es el área de la sección del conducto por donde circula el fluido y v su velocidad media.
En el caso de fluidos compresibles, donde la ecuación de Bernouilli no es válida, es necesario utilizar la formulación más completa de Navier y Stokes. Estas ecuaciones son la expresión matemática de la conservación de masa y de cantidad de movimiento. Para fluidos compresibles pero no viscosos, también llamados fluidos coloidales, se reducen a las ecuaciones de Euler.
Daniel Bernoulli fue un matemático que realizó estudios de dinámica.
La hidrodinámica o fluidos en movimientos presenta varias características que pueden ser descritas por ecuaciones matemáticas muy sencillas.
Ley de Torricelli: si en un recipiente que no está tapado se encuentra un fluido y se le abre al recipiente un orificio la velocidad con que caerá ese fluido será:
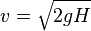
La otra ecuación matemática que describe a los fluidos en movimiento es el número de Reynolds:
N = dVD / n
donde d es la densidad v la velocidad D es el diámetro del cilindro y n es la viscosidad.
Presión hidrodinámica
En un fluido en movimiento general, al medir la presión según diferentes direcciones alrededor de un punto esta no será constante, dependiendo la dirección donde la presión es máxima y mínima de la dirección y valor de la velocidad en ese punto.
De hecho en un fluido newtoniano cuya ecuación constitutiva, que relaciona el tensor tensión con el tensor velocidad de deformación:
Donde:
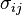 son las componentes del tensor tensión.
son las componentes del tensor tensión.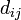 son las componentes del tensor velocidad de deformación.
son las componentes del tensor velocidad de deformación.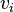 son las componentes del vector velocidad del fluido.
son las componentes del vector velocidad del fluido.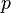 es la presión hidrodinámica.
es la presión hidrodinámica.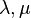 son dos viscosidades que caracterizan el comportamiento del fluido.
son dos viscosidades que caracterizan el comportamiento del fluido.Puede probarse que la presión hidrodinámica se relaciona con la presión media por:
Donde:
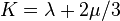 , es la viscosidad volumétrica.
, es la viscosidad volumétrica.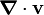 , es la divergencia del vector velocidad.
, es la divergencia del vector velocidad.

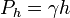
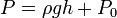
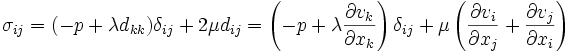
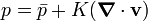
0 comentarios