Hidrostática

1. Variación de la presión con la profundidad

Todos los líquidos pesan, por ello cuando están contenidos en un recipiente las capas superiores oprimen a las inferiores, generándose una presión debida al peso. La presión en un punto determinado del líquido deberá depender entonces de la altura de la columna de líquido que tenga por encima suyo.

Considérese un líquido de densidad r en reposo y abierto a la atmósfera. Seleccionaremos una muestra de líquido contenida por un cilindro imaginario de área de sección transversal A que se extiende desde la superficie del líquido hasta una profundidad "h". La presión ejercida por el fluido sobre la cara inferior es P, y la presión sobre la cara superior del cilindro es la presión atmosférica, Po. Por consiguiente, la fuerza hacia arriba ejercida por el líquido sobre el fondo del cilindro es Pa, y la fuerza hacia abajo ejercida por la atmósfera sobre la parte superior es PoA. Debido a que la masa del líquido en el cilindro es r V = r Ah, el peso del fluido en el cilindro es w = r gv = r gAh. Como el cilindro está en equilibrio, la fuerza hacia abajo en la parte superior de la muestra para soportar su peso es igual a

Pa = Po + r gh ecc.7

(llamada ecuación fundamental de la hidrostática) ,donde la presión atm es 1,01 x 105 Pascales. En otras palabras la presión absoluta "Pa" una profundidad "h" debajo de la superficie de un líquido abierto a la atmósfera es mayor que la presión atmosférica en una cantidad r gh. Ello implica que ni la forma de un recipiente ni la cantidad de líquido que contiene influyen en la presión que se ejerce sobre su fondo, tan sólo la altura de líquido.

En vista del hecho de que la presión en un líquido sólo depende de la profundidad, cualquier incremento de presión en la superficie debe transmitirse a cada punto en el fluido. Esto lo reconoció por primera vez el científico Alemán Blaise Pascal (1923-1662) y se conoce como ley de Pascal (Página 18-22 Maiztegui-Sabato).

Aplicación:

Un submarinista se sumerge en el mar hasta alcanzar una profundidad de 100 m. Determinar la presión a la que está sometido y calcular en cuántas veces supera a la que experimentaría en el exterior, sabiendo que la densidad del agua del mar es de 1025 kg/m3.

Solución:

De acuerdo con la ecuación fundamental de la hidrostática:

Considerando que la presión Po en el exterior es de una atmósfera (1 atm = 1,013 x 105 Pa), al sustituir los datos en la anterior ecuación resulta:

P = 1,013x105 Pa+ 1025 kg/m3 x 9,8 m/s2 · 100 m = 11,058x105 Pa

El número de veces que P es superior a la presión exterior Po se obtiene hallando el cociente entre ambas lo que indica que es 10,9 veces superior la presión Pa.

2. El principio de Pascal y sus aplicaciones

La presión aplicada en un punto de un líquido contenido en un recipiente se transmite con el mismo valor a cada una de las partes del mismo.

Este enunciado, obtenido a partir de observaciones y experimentos por el físico y matemático B. Pascal, se conoce como principio de Pascal.

El principio de Pascal puede ser interpretado como una consecuencia de la ecuación fundamental de la hidrostática y del carácter incompresible de los líquidos. En esta clase de fluidos la densidad es constante, de modo que de acuerdo con la ecuación P = Po + r gh si se aumenta la presión en la superficie libre, por ejemplo, la presión en el fondo ha de aumentar en la misma medida, ya que r g no varía al no hacerlo h.

La prensa hidráulica constituye la aplicación fundamental del principio de Pascal y también un dispositivo que permite entender mejor su significado. Consiste, en esencia, en dos cilindros de diferente sección comunicados entre sí, y cuyo interior está completamente lleno de un líquido que puede ser agua o aceite. Dos émbolos de secciones diferentes se ajustan, respectivamente, en cada uno de los dos cilindros, de modo que estén en contacto con el líquido. Cuando sobre el émbolo de menor sección A1 se ejerce una fuerza F1 la presión P1 que se origina en el líquido en contacto con él se transmite íntegramente y de forma instantánea a todo el resto del líquido; por tanto, será igual a la presión P2 que ejerce el líquido sobre el émbolo de mayor sección A2, es decir:

P1 = P2

Si la sección A2 es veinte veces mayor que la A1, la fuerza F1 aplicada sobre el émbolo pequeño se ve multiplicada por veinte en el émbolo grande.

La prensa hidráulica es una máquina simple semejante a la palanca de Arquímedes, que permite amplificar la intensidad de las fuerzas y constituye el fundamento de elevadores, prensas, frenos y muchos otros dispositivos hidráulicos de maquinaria industrial.

Ejemplo programado:

Con referencia a la figura 1 (prensa hidráulica), las áreas del pistón A y del cilindro B, son respectivamente de 40 y 4000 cm2 y B pesa 4000 Kg. Los depósitos y las conducciones con conexión están llenas de aceite con una densidad de 750 kg/cm3 ¿Cuál es la Fuerza en A (en la Presión a) necesaria para mantener el equilibrio si se desprecia el peso de A?

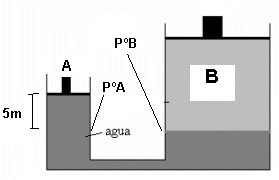
Figura 1. Ejercicio Prensa Hidráulica

Solución:

Pa + 750 kg/m3 x 5 m = 4000 Kg/4000 cm2

Pa + 3750Kg/100*100 cm2 = 1 Kg/cm2

Pa = 0,625 Kg/cm2

Presión = F x área (40cm2)= F = 25 Kg es la fuerza en A (en la Presión a) necesaria para mantener el equilibrio el sistema.

3. El principio de los vasos comunicantes

Si se tienen dos recipientes comunicados y se vierte un líquido en uno de ellos en éste se distribuirá entre ambos de tal modo que, independientemente de sus capacidades, el nivel de líquido en uno y otro recipiente sea el mismo. Éste es el llamado principio de los vasos comunicantes, que es una consecuencia de la ecuación fundamental de la hidrostática.

Si se toman dos puntos A y B situados en el mismo nivel, sus presiones hidrostáticas han de ser las mismas, es decir:

luego si Pa = Pb necesariamente las alturas ha y hb de las respectivas superficies libres han de ser idénticas ha = hb.

Si se emplean dos líquidos de diferentes densidades y no miscibles, entonces las alturas serán inversamente proporcionales a las respectivas densidades. En efecto, se tiene:

Pa + r gh = Pb + r gh ecc.8

Esta ecuación permite, a partir de la medida de las alturas, la determinación experimental de la densidad relativa de un líquido respecto de otro y constituye, por tanto, un modo de medir densidades de líquidos no miscibles si la de uno de ellos es conocida.

4. Empuje hidrostático: principio de Arquímedes

Los cuerpos sólidos sumergidos en un líquido experimentan un empuje hacia arriba. Este fenómeno, que es el fundamento de la flotación de los barcos, era conocido desde la más remota antigüedad, pero fue el griego Arquímedes (287-212 a. de C.) quien indicó cuál es la magnitud de dicho empuje. De acuerdo con el principio que lleva su nombre, todo cuerpo sumergido total o parcialmente en un líquido experimenta un empuje vertical y hacia arriba igual al peso del volumen de líquido desalojado.

El principio de Arquímedes puede comprobarse de la siguiente manea. Supóngase que centramos nuestra atención en el cubo de fluido dentro del recipiente de la figura ( ). Este cubo de fluido está en equilibrio bajo la acción de las fuerzas que actúan sobre él. Una de ellas es su peso. ¿Qué cancela la fuerza hacia abajo? Aparentemente, el resto del fluido dentro del recipiente se mantiene en equilibrio. Así, la fuerza de flotación "B" sobre el cubo de fluido es exactamente igual en magnitud al peso del fluido dentro del cubo:

E = w ecc. 6

Ahora mostraremos explícitamente que la fuerza de flotación es igual en magnitud al peso del fluido desplazado. La presión en el fondo del cubo en la figura 2 es más grande que la presión en la parte superior por una cantidad r fgh, donde r f es la densidad del fluido y h es la altura del cubo. Puesto que la diferencia de presión, D P, es igual a la fuerza de flotación por unidad de área, es decir, D P =E/A, vemos que E = (D P)A = (r fgh)A = r fgV, donde V es el volumen del cubo. Puesto que la masa del fluido en el cubo es m = r fV, vemos que

E = W = r f ecc.9

donde W es el peso del fluido desplazado.

<> Figura 2. W = E

Caso I. Un objeto sumergido totalmente. Cuando un objeto está totalmente sumergido en un fluido de densidad r f la fuerza de flotación hacia arriba está dada por E = r fVog; donde Vo es el volumen del objeto. Si el objeto tiene una densidad r o, su peso es igual a w = mg = r o Vog y la fuerza neta sobre él es E-w = (r f -r o)Vog. Por lo tanto, si la densidad del objeto es menor que la densidad del fluido, como la figura 3a, el objeto es mayor que la densidad del fluido, como la figura 3b, el objeto se hundirá.

<>

a) Un objeto totalmente sumergido que es menos denso que el fluido en el que está inmerso experimentará una fuerza neta hacia arriba

<> b) Un objeto sumergido totalmente que es más denso que el fluido se hunde.

Figura 3a y 3b. Objeto sumergido totalmente

Caso II. Un Objeto en flotación. Consideremos un objeto en equilibrio estático que flota en un fluido, es decir, un objeto parcialmente sumergido. En este caso, la fuerza de flotación hacia arriba se equilibra con el peso hacia abajo del objeto. Si V es el volumen del fluido desplazado por el objeto (el cual corresponde al volumen del objeto del nivel del fluido), entonces la fuerza de flotación tiene una magnitud E = r fVg. Puesto que el peso del objeto es W = mg = r o Vog y w = E, vemos que r fVg = r o Vog ó

r o/r f = V/Vo<> ecc.10

Ejemplo programado:

En un vaso de vidrio lleno de agua, flota un cubo de hielo. ¿Qué fracción del cubo sobresale del nivel de agua?.

Solución:

Este problema corresponde al caso II descrito anteriormente. El peso del cubo de hielo es W = r iVig, donde r i = 917 Kg/m3 y Vi = es el volumen del cubo de hielo. La fuerza de flotación hacia arriba es igual al peso del agua desplazada; es decir, E = r wVg, donde V es el volumen del cubo de hielo debajo del agua y r w es la densidad del agua, que es 1000 Kg/m3.

Como r iVig = r wVg, la fracción de hielo debajo del agua es V/Vi = r i/r w. Por consiguiente, la fracción de hielo sobre el nivel de agua es:

V/Vi = 917 (Kg/m3) /1000 (Kg/m3) = 0,917

V/Vi = 0,917

Por lo que el cubo de hielo tiene un 91,7% sumergido y un 8,3% sobre el nivel del agua.

5. Presión manométrica y absoluta

Cuando se realizan cálculos que implican la presión de un fluido, se debe hacer la medición en relación con alguna presión de referencia. Normalmente, la presión de referencia es la atmosférica, y la presión resultante que se mide se conoce como PRESIÓN MANOMÉTRICA. La presión que se mide con relación con el vacío perfecto se conoce con el nombre de PRESIÓN ABSOLUTA.

P absoluta = P manométrica + P atmosférica ecc.11

Ejemplo programado::

Exprese una presión de 155 Kpa como una presión absoluta. La presión atmosférica local es de 98 Kpa.

Solución:

P abs = P Mno + P atm

P abs = 155 Kpa + 98 Kpa = 253 Kpa

Un manómetro es un aparato que sirve para medir la presión de los fluidos contenidos en recipientes cerrados. Existen, básicamente, dos tipos de manómetros: los de líquidos y los metálicos.

Los manómetros de líquidos emplean, por lo general, mercurio que llena un tubo en forma de J. El tubo puede estar o abierto por ambas ramas o abierto por una sola. En ambos casos la presión se mide conectando al recipiente que contiene el gas el tubo por su rama inferior y abierta y determinando el desnivel h de la columna de mercurio entre ambas ramas. Si el manómetro es de tubo abierto entonces es necesario tomar en cuenta la presión atmosférica Po en la ecuación P = Po + r gh. Si es de tubo cerrado, la presión vendrá dada directamente por P = r gh. Los manómetros de este segundo tipo permiten, por sus características, la medida de presiones elevadas.

En los manómetros metálicos la presión del gas da lugar a deformaciones en una cavidad o tubo metálico. Estas deformaciones se transmiten a través de un sistema mecánico a una aguja que marca directamente la presión del gas sobre una escala graduada.

Hidrodinámica

El fluido como un continuo

Un fluido es una sustancia que se deforma continuamente al ser sometida a un esfuerzo cortante (esfuerzo tangencial) no importa cuan pequeño sea.

Todos los fluidos están compuestos de moléculas que se encuentran en movimiento constante. Sin embargo, en la mayor parte de las aplicaciones de ingeniería, nos interesa más conocer el efecto global o promedio (es decir, macroscópico) de las numerosas moléculas que forman el fluido. Son estos efectos macroscópicos los que realmente podemos percibir y medir.

Por lo anterior, consideraremos que el fluido está idealmente compuesto de una sustancia infinitamente divisible (es decir, como un continuo) y no nos preocuparemos por el comportamiento de las moléculas individuales.

El concepto de un continuo es la base de la mecánica de fluidos clásica. La hipótesis de un continuo resulta válida para estudiar el comportamiento de los fluidos en condiciones normales. Sin embargo, dicha hipótesis deja de ser válida cuando la trayectoria media libre de las moléculas (aproximadamente 6,3 x 10-5 mm o bien 2.5 x 10-6 pulg para aire en condiciones normales de presión y temperatura) resulta del mismo orden de magnitud que la longitud significativa más pequeña, característica del problema en cuestión.

Una de las consecuencias de la hipótesis del continuo es que cada una de las propiedades de un fluido se supone que tenga un valor definido en cada punto del espacio. De esta manera, propiedades como la densidad, temperatura, velocidad, etc., pueden considerarse como funciones continuas de la posición y del tiempo.

1. Hemos definido un fluido como una sustancia que se deforma continuamente bajo la acción de un esfuerzo cortante. En ausencia de éste, no existe deformación. Los fluidos se pueden clasificar en forma general, según la relación que existe entre el esfuerzo cortante aplicado y la rapidez de deformación resultante. Aquellos fluidos donde el esfuerzo cortante es directamente proporcional a la rapidez de deformación se denominan fluidos newtonianos. La mayor parte de los fluidos comunes como el agua, el aire, y la gasolina son prácticamente newtonianos bajo condiciones normales. El término no newtoniano se utiliza para clasificar todos los fluidos donde el esfuerzo cortante no es directamente proporcional a la rapidez de deformación.

   Numerosos fluidos comunes tienen un comportamiento no newtoniano. Dos ejemplos muy claros son la crema dental y la pintura Lucite. Esta última es muy "espesa" cuando se encuentra en su recipiente, pero se "adelgaza" si se extiende con una brocha. De este modo, se toma una gran cantidad de pintura para no repetir la operación muchas veces. La crema dental se comporta como un "fluido" cuando se presiona el tubo contenedor. Sin embargo, no fluye por sí misma cuando se deja abierto el recipiente. Existe un esfuerzo limite, de cedencia, por debajo del cual la crema dental se comporta como un sólido. En rigor, nuestra definición de fluido es válida únicamente para aquellos materiales que tienen un valor cero para este esfuerzo de cedencia. En este texto no se estudiarán los fluidos no newtonianos.

2. Fluidos Newtonianos y No Newtonianos
3. Viscosidad

Si se considera la deformación de dos fluidos newtonianos diferentes, por ejemplo, glicerina y agua, se encontrará que se deforman con diferente rapidez para una misma fuerza cortante. La glicerina ofrece mucha mayor resistencia a la deformación que el agua; se dice entonces que es mucho más viscosa.

La VISCOSIDAD DINÁMICA (u), se presenta cuando un fluido se mueve y se desarrolla en el una tensión de corte, denotada con la letra griega "t" (tao), y puede definirse como la fuerza requerida para deslizar una capa de área unitaria de una sustancia sobre otra capa de la misma sustancia. En un fluido común, como el agua, el aceite o alcohol encontramos que la magnitud de corte es directamente proporcional al cambio de velocidad entre diferentes posiciones del fluido. En el cuadro 2 se presentan valores de viscosidad dinámica para distintos fluidos.

CUADRO 2. Valores de viscosidad dinámica para algunos fluidos

 

Fluido	Temperatura (ºC)	V. Dinámica u (Ns/m2)
Agua	20	1 x 10-3
Gasolina	20	3,1 x 10-4
Aceite SAE 30	30	3,5 x 10-1
Aceite SAE 30	80	1,9 x 10-2

En la mecánica de fluidos se emplea muy frecuentemente la VISCOSIDAD CINEMÁTICA

v = u/r ecc.12

donde u viscosidad dinámica y las dimensiones en el SI que resultan para v son [m2/s].

La viscosidad es una manifestación del movimiento molecular dentro del fluido. Las moléculas de regiones con alta velocidad global chocan con las moléculas que se mueven con una velocidad global menor, y viceversa. Estos choques permiten transportar cantidad de movimiento de una región de fluido a otra. Ya que los movimientos moleculares aleatorios se ven afectados por la temperatura del medio, la viscosidad resulta ser una función de la temperatura 

Descripción y clasificación de los movimientos de un fluido

Antes de proceder con un análisis, intentaremos una clasificación general de la mecánica de fluidos sobre la base de las características físicas observables de los campos de flujo. Dado que existen bastantes coincidencias entre unos y otros tipos de flujos, no existe una clasificación universalmente aceptada. Una posibilidad es la que se muestra en la figura 4.

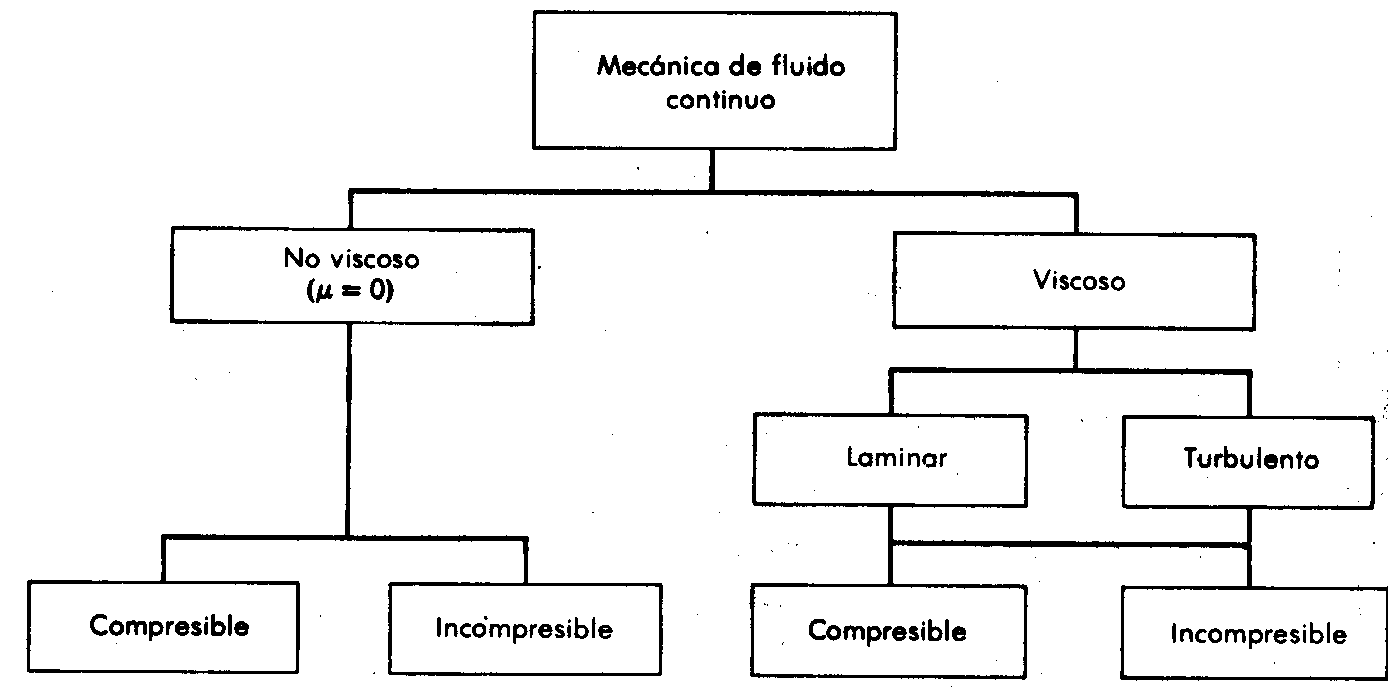
Figura 4. Esquema general de Fluidos continuos

3.1. Flujos Viscosos y no Viscosos

La subdivisión principal señalada en la figura anterior se tiene entre los flujos viscosos y no viscosos. En un flujo no viscoso se supone que la viscosidad de fluido u, vale cero. Evidentemente, tales flujos no existen; sin embargo; se tienen numerosos problemas donde esta hipótesis puede simplificar el análisis y al mismo tiempo ofrecer resultados significativos. (Si bien, los análisis simplificados siempre son deseables, los resultados deben ser razonablemente exactos para que tengan algún valor.) Dentro de la subdivisión de flujo viscoso podemos considerar problemas de dos clases principales. Flujos llamados incompresibles, en los cuales las variaciones de densidad son pequeñas y relativamente poco importantes. Flujos conocidos como compresibles donde las variaciones de densidad juegan un papel dominante como es el caso de los gases a velocidades muy altas.

Por otra parte, todos los fluidos poseen viscosidad, por lo que los flujos viscosos resultan de la mayor importancia en el estudio de mecánica de fluidos.

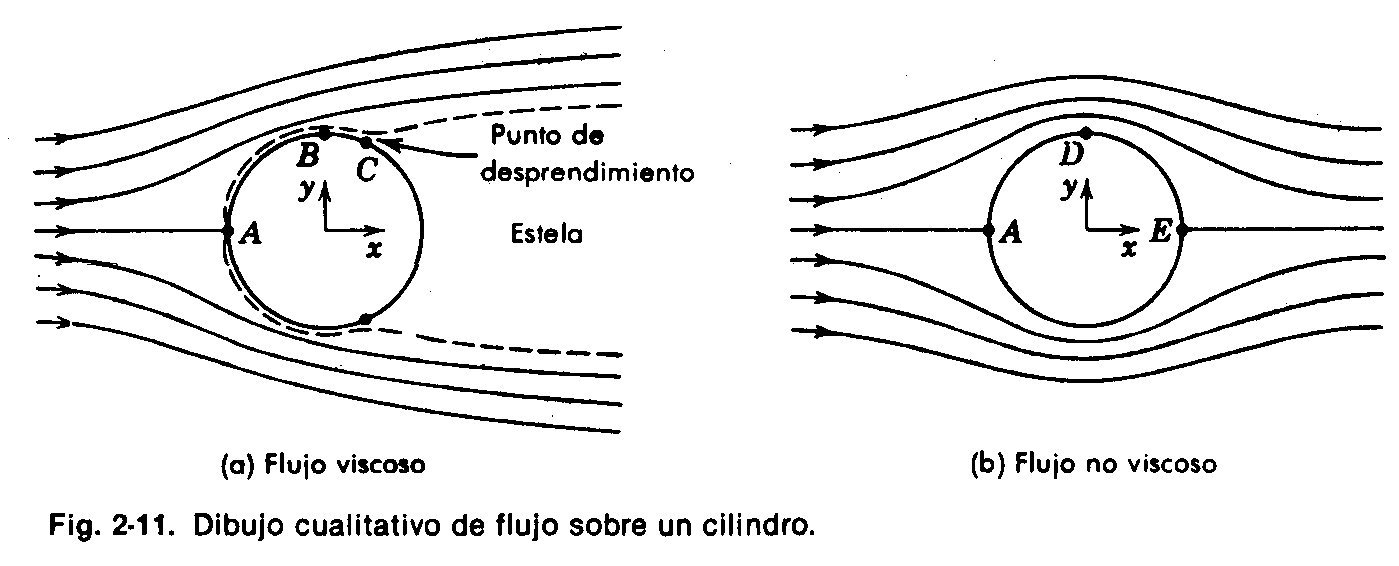
Figura 4. Dibujo cualitativo de flujo sobre un cilindro

Podemos observar que las líneas de corriente son simétricas respecto al eje x. El fluido a lo largo de la línea de corriente central se divide y fluye alrededor del cilindro una vez que ha incidido en el punto A. Este punto sobre el cilindro recibe el nombre de punto de estancamiento. Al igual que en el flujo sobre una placa plana, se desarrolla una capa límite en las cercanías de la pared sólida del cilindro. La distribución de velocidades fuera de la capa límite se puede determinar teniendo en cuenta el espaciamiento entre líneas de corriente. Puesto que no puede haber flujo a través de una línea de corriente, es de esperarse que la velocidad del fluido se incremente en aquellas regiones donde el espaciamiento entre líneas de corrientes disminuya. Por el contrario, un incremento en el espaciamiento entre líneas de corriente implica una disminución en la velocidad del fluido.

Considérese momentáneamente el flujo incompresible alrededor del cilindro, suponiendo que se trate de un flujo no viscoso, como el mostrado en la figura 4b, este flujo resulta simétrico respecto tanto al eje x como al eje y. La velocidad alrededor del cilindro crece hasta un valor máximo en el punto D y después disminuye conforme nos movemos alrededor del cilindro. Para un flujo no viscoso, un incremento en la velocidad siempre va acompañado de una disminución en la presión, y viceversa. De esta manera, en el caso que nos ocupa, la presión sobre la superficie del cilindro disminuye conforme nos movemos del punto A al punto D y después se incrementa al pasar del punto D hasta el E. Puesto que el flujo es simétrico respecto a los dos ejes coordenados, es de esperarse que la distribución de presiones resulte también simétrica respecto a estos ejes. Este es, en efecto, el caso.

No existiendo esfuerzos cortantes en un flujo no viscoso, para determinar la fuerza neta que actúa sobre un cilindro solamente se necesita considerar las fuerzas de presión. La simetría en la distribución de presiones conduce a la conclusión de que en un flujo no viscoso no existe una fuerza neta que actúe sobre un cilindro, ya sea en la dirección x o en la dirección y. La fuerza neta en la dirección x recibe el nombre de arrastre. Según lo anterior, se concluye que el arrastre para un cilindro en un flujo no viscoso es cero; esta conclusión evidentemente contradice nuestra experiencia, ya que sabemos que todos los cuerpos sumergidos en un flujo real experimentan algún arrastre. Al examinar el flujo no viscoso alrededor de un cuerpo hemos despreciado la presencia de la capa límite, en virtud de la definición de un flujo no viscoso. Regresemos ahora a examinar el caso real correspondiente.

Para estudiar el caso real de la figura 4a, supondremos que la capa límite es delgada. Si tal es el caso, es razonable suponer además que el campo de presiones es cualitativamente el mismo que en el correspondiente flujo no viscoso. Puesto que la presión disminuye continuamente entre los puntos A y B un elemento de fluido dentro de la capa límite experimenta una fuerza de presión neta en la dirección del flujo. En la región entre A y B, esta fuerza de presión neta es suficiente para superar la fuerza cortante resistente, manteniéndose el movimiento del elemento en la dirección del flujo.

Considérese ahora un elemento de fluido dentro de la capa límite en la parte posterior del cilindro detrás del punto B. Puesto que la presión crece en la dirección del flujo, dicho elemento de fluido experimenta una fuerza de presión neta opuesta a la dirección del movimiento. En algún punto sobre el cilindro, la cantidad de movimiento del fluido dentro de la capa limite resulta insuficiente para empujar al elemento más allá dentro de la región donde crece la presión. Las capas de fluido adyacentes a la superficie del sólido alcanzarán el reposo, y el flujo se separará de la superficie; el punto preciso donde esto ocurre se llama punto de separación o desprendimiento. La separación de la capa límite da como resultado la formación de una región de presión relativamente baja detrás del cuerpo; esta región resulta deficiente también en cantidad de movimiento y se le conoce como estela. Se tiene, pues, que para el flujo separado alrededor de un cuerpo, existe un desbalance neto de las fuerzas de presión, en la dirección del flujo dando como resultado un arrastre debido a la presión sobre el cuerpo. Cuanto mayor sea el tamaño de la estela detrás del cuerpo, tanto mayor resultará el arrastre debido a la presión.

Es lógico preguntarnos cómo se podría reducir el tamaño de la estela y por lo tanto el arrastre debido a la presión. Como una estela grande surge de la separación de la capa límite, y este efecto a su vez se debe a la presencia de un gradiente de presión adverso (es decir, un incremento de presión en la dirección del flujo), la reducción de este gradiente adverso debe retrasar el fenómeno de la separación y, por tanto, reducir el arrastre.

El fuselado de un cuerpo reduce la magnitud del gradiente de presión adverso al distribuirlo sobre una mayor distancia. Por ejemplo, si se añadiese una sección gradualmente afilada (cuña) en la parte posterior del cilindro de

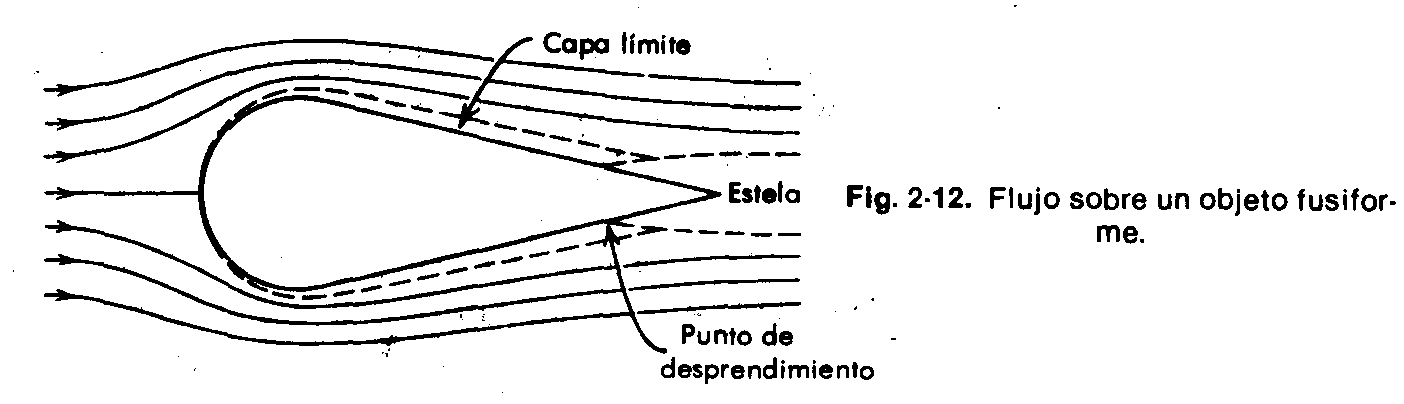
Figura 5. Flujo sobre un objeto fusiforme

la figura 4, el flujo cualitativamente sería como se muestra en la figura 5. El fuselaje en la forma del cuerpo efectivamente retrasa el punto de separación, si bien la superficie del cuerpo expuesta al flujo y, por lo tanto, la fuerza cortante total que actúa sobre el cuerpo, se ven incrementadas, el arrastre total se ve reducido de manera significativa.

La separación del flujo se puede presentar también en flujos internos (es decir, flujos a través de ductos) como resultado de cambios bruscos en la geometría del ducto.

3.2. Flujos laminares y turbulentos

Los flujos viscosos se pueden clasificar en laminares o turbulentos teniendo en cuenta la estructura interna del flujo. En un régimen laminar, la estructura del flujo se caracteriza por el movimiento de láminas o capas. La estructura del flujo en un régimen turbulento por otro lado, se caracteriza por los movimientos tridimensionales, aleatorios, de las partículas de fluido, superpuestos al movimiento promedio.

En un flujo laminar no existe un estado macroscópico de las capas de fluido adyacentes entre sí. Un filamento delgado de tinta que se inyecte en un flujo laminar aparece como una sola línea; no se presenta dispersión de la tinta a través del flujo, excepto una difusión muy lenta debido al movimiento molecular. Por otra parte, un filamento de tinta inyectado en un flujo turbulento rápidamente se dispersa en todo el campo de flujo; la línea del colorante se descompone en una enredada maraña de hilos de tinta. Este comportamiento del flujo turbulento se debe a las pequeñas fluctuaciones de velocidad superpuestas al flujo medio de un flujo turbulento; el mezclado macroscópico de partículas pertenecientes a capas adyacentes de fluido da como resultado una rápida dispersión del colorante. El filamento rectilíneo de humo que sale de un cigarrillo expuesto a un ambiente tranquilo, ofrece una imagen clara del flujo laminar. Conforme el humo continúa subiendo, se transforma en un movimiento aleatorio, irregular; es un ejemplo de flujo turbulento.

El que un flujo sea laminar o turbulento depende de las propiedades del caso. Así, por ejemplo, la naturaleza del flujo (laminar o turbulento) a través de un tubo se puede establecer teniendo en cuenta el valor de un parámetro adimensional, el número de Reynolds,

Re = r VD/u, ecc.13

donde r es la densidad del fluido, V la velocidad promedio, D el diámetro del tubo y u la viscosidad.

El flujo dentro de una capa límite puede ser también laminar o turbulento; las definiciones de flujo laminar y flujo turbulento dadas anteriormente se aplican también en este caso. Las características de un flujo pueden ser significativamente diferentes dependiendo de que la capa límite sea laminar o turbulenta. Los métodos de análisis también son diferentes para un flujo laminar que para un flujo turbulento. Por lo tanto, al iniciar el análisis de un flujo dado es necesario determinar primero si se trata de un flujo laminar o de un flujo turbulento.

3.3. Flujo compresible e incompresible

Aquellos flujos donde las variaciones en densidad son insignificantes se denominan incompresibles; cuando las variaciones en densidad dentro de un flujo no se pueden despreciar, se llaman compresibles. Si se consideran los dos estados de la materia incluidos en la definición de fluido, líquido y gas, se podría caer en el error de generalizar diciendo que todos los flujos líquidos son flujos incompresibles y que todos los flujos de gases son flujos compresibles.

La primera parte de esta generalización es correcta para la mayor parte de los casos prácticos, es decir, casi todos los flujos líquidos son esencialmente incompresibles. Por otra parte, los flujos de gases se pueden también considerar como incompresibles si las velocidades son pequeñas respecto a la velocidad del sonido en el fluido; la razón de la velocidad del flujo, V, a la velocidad del sonido, c, en el medio fluido recibe el nombre de número de Mach, M, es decir,

M=V/c ecc. 14

Los cambios en densidad son solamente del orden del 2% de valor medio, para valores de M < 0,3. Así, los gases que fluyen con M < 0,3 se pueden considerar como incompresibles; un valor de M = 0,3 en el aire bajo condiciones normales corresponde a una velocidad de aproximadamente 100 m/s.

Los flujos compresibles se presentan con frecuencia en las aplicaciones de ingeniería. Entre los ejemplos más comunes se pueden contar los sistemas de aire comprimido utilizados en la operación de herramienta